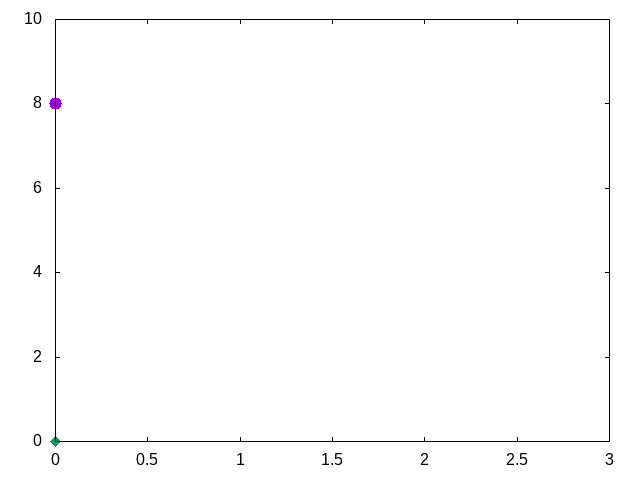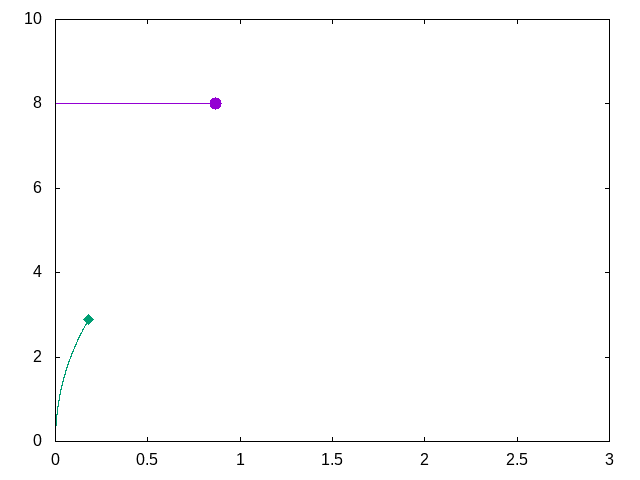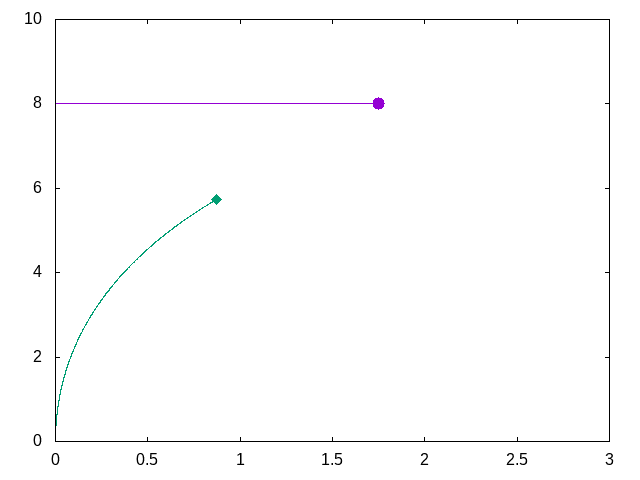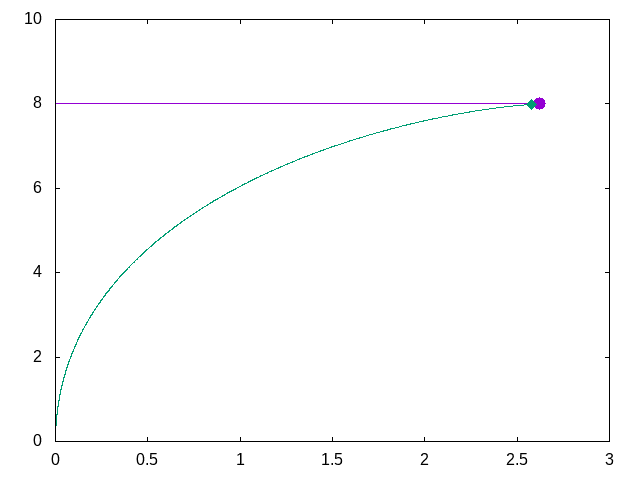
It seems obvious that I need to construct some equations to integrate over time in order to account for the movement of missile. Most importantly, the change of angle over time.
Layout the basics
I started with a sketch:
$\theta = \arctan(\cfrac{8-y}{600t-x})$
$\cos(\theta) = \cfrac{1}{\sqrt{1 + \cfrac{(8-y)^2}{(600t-x)^2}}}$
$\sin(\theta) = \cfrac{8-y}{(600t - x)\sqrt{1 + \cfrac{(8-y)^2}{(600t-x)^2}}}$
| Derivatives |
Description |
| $\frac{dz}{dt} = 2000 km/h$ |
The missile’s total speed. |
| $\frac{dx}{dt} = 2000*\cos(\theta) km/h$ |
The missile’s horizontal speed. |
| $\frac{dy}{dt} = 2000*\sin(\theta) km/h$ |
The missile’s vertical speed. |
| $\frac{dx}{dt} * \frac{dt}{dy} = \frac{dx}{dy}$ |
Do arithmetic with above values. |
| $\frac{dx}{dy} = \cfrac{600t - x}{8-y}$ |
Rate of change of horizontal / vertical speed. |
| $\frac{dz}{dy} = \sqrt{1 + (\frac{dx}{dy})^2}$ |
 |
Begin to solve
At present to have too many variables. Let’s see if we can simplify the problem.
$$\frac{dx}{dy} = \cfrac{600t - x}{8-y}$$
We can take the derivative with respect to $y$ of the equation above.
$$\frac{d}{dy}\lgroup(8-y)\frac{dx}{dy} = 600t - x\rgroup$$
With the product rule we find:
$$(8-y)\frac{dx^2}{d^2y} {\color{red} -\frac{dx}{dy} } = 600\cfrac{dt}{dy} {\color{red} -\frac{dx}{dy} }$$
Let’s substitute $\cfrac{dt}{dy}$ out with $\cfrac{dt}{dz} * \cfrac{dz}{dy} = \cfrac{\sqrt{1 + (\frac{dx}{dy})^2}}{2000}$ from our table above.
$$(8-y)\frac{dx^2}{d^2y} = 600\cfrac{\sqrt{1 + (\frac{dx}{dy})^2}}{2000}$$
let $u = \frac{dx}{dy}$ and substitute
$$(8-y)\frac{du}{dy} = \frac{3}{10} \sqrt{1 + u^2}$$
This can be written as a separable differential equation.
Alternative Solution 1
$$\int{\frac{1}{\sqrt{1 + u^2}} du} = \frac{3}{10} \int{\cfrac{1}{8-y}dy}$$
This can be solved directly:
$$\ln{(\sqrt{1 + u^2} + u)} = \frac{-3}{10} \ln{(8-y)} + \ln{(c)}$$
We cheated here a a bit and set our constant as $\ln{c}$ instead of $c$ to take advantage of some log rules later.
Exponentiating both sides we get:
$${\color{red}e}^{\ln{(\sqrt{1 + u^2} + u)}} = {\color{red}e}^{\frac{-3}{10} \ln{(8-y)} + \ln{(c)}}$$
$$\sqrt{1 + u^2} + u = \cfrac{c}{(8-y)^\frac{3}{10}}$$
At $t=0$, the missile is pointing up so $dx = 0$ thus $u = 0$, $y = 0$ as well (missile on ground):
$$c = 8^\frac{3}{10}$$
With so much latex to write, let me copy the strokes from my OneNote:
Long calculations

This yields us a final function of:
$$x = \frac{1}{2} (8^{\frac{3}{10}}(-\frac{(8-y)^{\frac{7}{10}}}{\frac{7}{10}}) + \frac{(8-y)^{\frac{13}{10}}}{\frac{13}{10}(8^{\frac{3}{10}})}) + k$$
$k$ is our new constant to solve for.
At $t=0$, $x = 0$ & $y = 0$ thus $k = 2.64$
Alternative Solution 2
$$\int{\frac{1}{\sqrt{1 + u^2}} du} = \frac{3}{10} \int{\cfrac{1}{8-y}dy}$$
In this path we observe that the left side of the integral can be expressed as the inverse hyperbolic sine.
$$\sinh^{-1}(u) = \frac{-3}{10} \ln{(8-y)} + \ln{(c)}$$
Exponentiating both sides we get:
$${\color{red}e}^{\sinh^{-1}(u)} = {\color{red}e}^{\ln(\frac{c}{(8-y)^{\frac{3}{10}}})}$$
Simplifying:
$$e^{\sinh^{-1}(u)} = \frac{c}{(8-y)^{\frac{3}{10}}}$$
Solve for $c$ by setting $x$ & $y = 0$:
$$c = 8^{\frac{3}{10}}$$
Solve for $u$ and substitute in $c$:
$$\sinh^{-1}(u) = \ln(\frac{c}{(8-y)^{\frac{3}{10}}})$$
$$u = \sinh(\ln(\frac{8^{\frac{3}{10}}}{(8-y)^{\frac{3}{10}}}))$$
Note the definition of the $\sinh(a)$:
$$\sinh(a) = \frac{e^{a} - e^{-a}}{2}$$
Substitute $\frac{dx}{dy}$ back in for $u$ and use the above definition of $\sinh$:
$$\frac{dx}{dy} = \frac{e^{\ln(\frac{8^{\frac{3}{10}}}{(8-y)^{\frac{3}{10}}})} - e^{\ln(\frac{(8-y)^{\frac{3}{10}}}{8^{\frac{3}{10}}})}}{2}$$
This yields us a separable differential equation which we can integrate. The final integral is a bit different looking but obviously goes to the same values.
$$\int{dx} = \int{e^{\ln{(\frac{8^{\frac{3}{10}}}{(8-y)^{\frac{3}{10}}})}} - e^{\ln{(\frac{(8-y)^{\frac{3}{10}}}{8^{\frac{3}{10}}})}}dy}$$
While complex looking it yields a direct answer in Wolfram Alpha
$$x = \frac{1}{2}(\frac{1.86607(1.42857y-11.4286)}{(8-y)^{\frac{3}{10}}} - 0.535887(8-y)^{\frac{3}{10}}(0.769231y-6.15385)) + k$$
$k$ is our new constant to solve for.
At $t=0$, $x = 0$ & $y = 0$ thus $k = 2.64$
As we can see, when $y$ approaches $8$ from the left, the right side expressions approaches divide by zero error. So, this solution has no answer at exactly collision time. It is fair however to say the missile hits the plane.

Analytical Solution
When $y = 8$, $x$ is the distance the plane traveled at collision time.
We plug $y = 8$ in above and solve for $x$.
$$x = 2.64km$$
The time is:
$$t = \frac{2.64km}{600\frac{km}{h}} = 0.0044h = 15.84s$$
The missile traveled:
$$2000\frac{km}{h} * 0.0044h = 8.8km$$
Numerical solution provided by my colleague Jeremy
My colleague Jeremy builds a tool called wasora. He wrote the script below to calculate the values for this problem numerically and generated the gif above. This tool is cool!
dt = 1e-5
end_time = 20
# problem parameters
h0 = 8 # plane height [miles]
vp = 600/3600 # plane speed [miles/second]
vm = 2000/3600 # missile speed [miles/second]
PHASE_SPACE xp yp theta xm ym s
# non-zero initial conditions
yp_0 = h0
theta_0 = pi/2
# DAE system
xp_dot .= vp
yp_dot .= 0
theta .= atan2(yp-ym, xp-xm)
xm_dot .= vm*cos(theta)
ym_dot .= vm*sin(theta)
s_dot .= sqrt(xm_dot^2+ym_dot^2)
# output
PRINT %.8f t xp yp xm ym theta s %e ((xm-xp)^2+(ym-yp)^2)
# termination condition
done = ((xm-xp)^2+(ym-yp)^2)<1e-12
IF done
PRINT "\# distance the plane traveled: " xp "miles"
PRINT "\# time to impact: " t "seconds"
PRINT "\# distance the missile traveled: " s "miles"
ENDIF