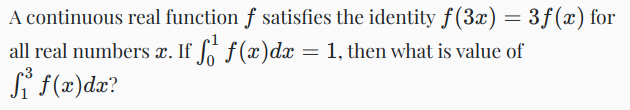Step 1: Assign a variable to the value we are solving for

$$ I = \int_1^3 f(x) dx $$

Step 2: Solve for $f(x)$

if $$ 3f(x) = f(3x) $$ then $$ f(x) = \frac{1}{3} f(3x) $$

Step 3: Solve for a portion of the definite integral we are after

$$ \int_\frac{1}{3}^1 f(x) dx = \int_\frac{1}{3}^1 \frac{1}{3} f(3x) dx $$

$$ \frac{1}{3} \int_\frac{1}{3}^1 f(3x) dx $$

Substitute $$ u=3x \newline dx=\frac{1}{3}du \newline \frac{1}{9} \int_1^3 f(u) du $$

Observe that $$\int_\frac{1}{3}^1 f(x) dx = \frac{1}{9} \int_1^3 f(u) du = \frac{1}{9} I$$

Step 4: Solve for ever smaller parts of the definite integral adjacent to the previous one

$$ \int_\frac{1}{9}^\frac{1}{3} f(x) dx = \int_\frac{1}{9}^\frac{1}{3} \frac{1}{3} f(3x) dx $$

$$ \frac{1}{3} \int_\frac{1}{9}^\frac{1}{3} f(3x) dx $$

Substitute $$ u=3x \newline dx=\frac{1}{3}du \newline \frac{1}{9} \int_\frac{1}{3}^1 f(u) du $$

Observe that $$\int_\frac{1}{9}^\frac{1}{3} f(x) dx = \frac{1}{9} \int_\frac{1}{3}^1 f(u) du = \frac{1}{9^2} I$$

Step 5: At this point we can see a pattern

$$\int_\frac{1}{3^n}^\frac{1}{3^{n-1}} f(x) dx = \frac{1}{9^n}I $$

We also know that at the limit this is equal to $\frac{1}{3^n} = 0$

Step 6: Create a geometric series

$$ \lim\limits_{n \to \infty} \Bigg( \int_\frac{1}{3}^1 f(x) dx + \int_\frac{1}{9}^\frac{1}{3} f(x) dx \dotsc \int_\frac{1}{3^n}^\frac{1}{3^{n-1}} f(x) dx \Bigg) = \lim\limits_{n \to \infty} \Bigg( \frac{1}{9}I + \frac{1}{9^2}I \dotsc \frac{1}{9^n}I \Bigg) = \int_0^1 f(x) dx = 1$$

$$ \displaystyle\sum_{n=1}^\infty \Bigg( \frac{1}{9^n}I \Bigg) = I\displaystyle\sum_{n=1}^\infty \Bigg( \frac{1}{9^n} \Bigg) = 1$$

This is a converging geometric series. The sum of the series is

$$\displaystyle\sum_{n=1}^\infty \Bigg( \frac{1}{9^n} \Bigg) = \frac{\frac{1}{9}}{1-\frac{1}{9}} = \frac{\frac{1}{9}}{\frac{8}{9}} = \frac{1}{8}$$

So

$$ \frac{1}{8}I = 1$$

$$ \boxed{I = \int_1^3 f(x) dx = 8 = 🤯}$$

Inspired by blackpenredpen

Your obedient servant,